Projekt Bungee Jump . Fysik
højniveau

Indholdsfortegnelse
Side 1 Indholdsfortegnelse
Side 1 Hvad
skal besvarelsen indeholde?
Side 2 Opvarmning
Side 3 Værktøjskasse
til brug senere
Side 4 1.
forsøg: Eftervisning af Hookes lov
Side 4 2. forsøg: Eftervisning af formlen for
potentiel fjederenergi. Bungee Jump.
Side 6 3. forsøg: Eftervisning af formlen for
potentiel fjederenergi. Omvendt
Bungee Jump.
Side 9 Tjek
for fejl ved forsøg 2 og 3
Side 9 4.
forsøg: Dæmpet harmonisk bevægelse, find dæmpningsfaktoren.
Side 12 5.
forsøg: Eftervisning af svingningstidsformlen, ved
anvendelse af
accelerometer.
Side 14 6. forsøg: Bungee
Jump med accelerometer.
Side 15 Teoretiske overvejelser
Hvad skal besvarelsen indeholde?
Alle skal i timen regne eksamensopgaven
under opvarmning. Den skal ikke med i raporten.
Alle skal udføre forsøg1 om Hookes lov, og skrive rapport om det.
Alle skal udføre to af
forsøgene 2-6, og skriv rapport om det.
Rapporten skal indeholde den
anvendte teori.
Opvarmning:
Start med at regne følgende
eksamensopgave:
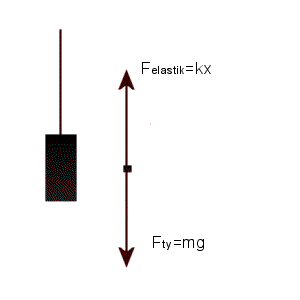
Elastikspring.

Et elastikspring foregår fra
en kran 54m over jorden, ( se figur ovenfor). Udspringeren er bundet til kranen
med en lang og kraftig elastik. Det første stykke falder udspringeren frit. Så
strammes elastikken, og udspringeren svinger op og ned nogle gange indtil han
hænger stille.
Udspringeren vejer 70kg.
Elastikken kan betragtes som en fjeder med fjederkonstanten 62N/m. Elastikken
har længde 18m, når den ikke er strammet.
I springets laveste punkt
befinder udspringeren sig 4,0m over jorden.
a) Find udspringerens fart,
når det frie fald er forbi efter 18m.
b) Beregn den højde over
jorden, som udspringeren befinder sig i, når svingningen er gået i stå.
c)Beregn størrelsen af
udspringerens acceleration i springets laveste punkt.
d)Find tabet i mekanisk
energi fra springets start til det laveste punkt under springet.
Værktøjskasse til brug senere:
a) Hvordan får man indlæst
programmet DataMate?
Datamate skal sendes fra CBL-2 til ARC på
TI-83-plus.
Forbind din lommeregner med CBL-2. Tast 2nd link og vælg Recive
på din TI-83 plus.Tast Transfer på CBL-2 . Programmet sendes nu fra CBL-2 til TI-83
plus.
Tast 2nd quit, når
overførslen er forbi. Tast APPS
for at finde programmet når du skal benytte det.
b) Hvordan læser jeg lister
ind i TI-Interactive ?
![]()
Klik på liste-ikonet
Forbind jeres lommeregner
med computeren.
Klik på Liste 1, Vælg
”file”, Vælg ”import”, Vælg ”from TI-calculator”,
Der kommer nu en oversigt
over hvad der ligger i lommeregneren , vælg nu liste 1 fra lommeregneren.
Læs tilsvarende liste 2 ind
i L2.
C)Hvordan fitter jeg med sinusfunktionen i TI-Interactive?
I skal lave en sinusregression på jeres måletal.
Vælg nu statistik-ikonen
![]()
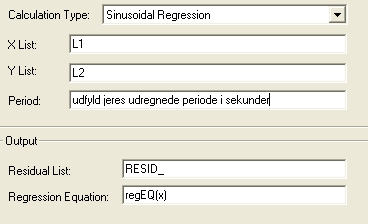
Udfyld skemaet
Tast calculate.
NB I alle forsøg nedenfor
benyttes samme elastiktype, og benyt samme længde elastik.
Vi vil starte med at
betragte et simplere problem nemlig en harmonisk svingning.
1. forsøg :
Eftervisning af Hookes lov:
Elastikken ophænges i et
stativ. Benyt en elastik på ca 1meters længde. Mål
elastikkens længde.
|
|
|
Hæng forskellige lodder på
elastikken og mål forlængelsen ![]() .
.
Mål 10 sammenhørende værdier
af massen m og forlængelsen ![]() .
.
Om fjederkraften gælder Hookes lov som lyder
: ![]() , hvor k er
fjederkonstanten for elastikken. ( NB loven gælder ikke generelt for elastikker med samme k for alle længder,
k afhænger af længden af elastikken, men holdes længden på en fast længde f.eks. 1m, så gælder Hookes lov
for en elastik på denne længde.)
, hvor k er
fjederkonstanten for elastikken. ( NB loven gælder ikke generelt for elastikker med samme k for alle længder,
k afhænger af længden af elastikken, men holdes længden på en fast længde f.eks. 1m, så gælder Hookes lov
for en elastik på denne længde.)
Der gælder ![]() for tyngdekraften.
for tyngdekraften.
Da loddet er i hvile har vi ![]() ó
ó ![]() .
.
Vi får derfor
(1) ![]()
Indtegn målepunkterne i TI-Interactive, lav en passende regression og bestem fjederkonstanten k for den benyttede elastik.
2. forsøg:
Eftervisning af formlen for potentiel fjederenergi. Bungee Jump.
Vi vil her se nærmere på
energien i en fjeder eller for os energien i en elastik.
Den potentielle fjederenergi der oplagres i
en fjeder er ![]() .
.
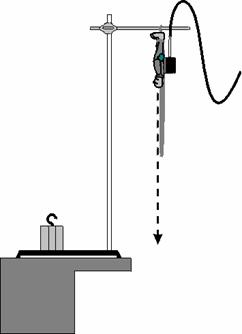
Benyt en flaske med vand, lad f.eks. massen af flaske med vand være 200g.
I skal benytte en målestok . Benyt en elastik på ca. en meter, hæng den
højt op.

Start med at lade elastikken hænge frit uden
flaske.
Mål afstanden x0 fra gulvet op til elastikken (absolut nulpunktet
for potentiel fjederenergi).
Sæt dernæst flasken på elastikken, mål
afstanden x1, fra gulvet til hvor flasken hænger i hvile i ligevægtsstillingen,
mål op til der hvor elastikken fæstnes.
Lad x være strækningen elastikken er trukket
ud. Der gælder da ![]() .
.
Dette punkt benyttes faktisk ikke, men det
er rart at vide hvor det er.
I ligevægtsstillingen er ![]() , dvs.
, dvs. ![]() , idet størrelsen af
tyngdekraften er lig størrelsen af fjederkraften.
, idet størrelsen af
tyngdekraften er lig størrelsen af fjederkraften.
Når vi løfter flasken over nulpunktet for
fjederen ( altså over det punkt hvor elastikken kan hænge helt frit uden
flaske), så vil vi have at den mekaniske energi er lig
![]() , hvor h1
er flaskens højde overgulvet.
, hvor h1
er flaskens højde overgulvet.
Vi kan se bort fra fjederen , idet
elastikken er slap , og der ikke er ophobet energi her.
Slipper vi flasken så den falder ned mod
gulvet, vil den opnå en ny højde h2.
Vi har nu ![]() , sidste led forsvinder, idet v=0 når flasken
, sidste led forsvinder, idet v=0 når flasken
vender i sin bevægelse.
x er
her igen strækningen elastikken er trukket ud. Der gælder her ![]() .
.
Lad nu ![]() være faldhøjden for
flasken.
være faldhøjden for
flasken.
Hvis vi antager energibevarelse får vi
![]() ó
ó
(2) ![]()
Løft nu flasken til en højde h1
over jorden, punktet skal være over det absolutte nulpunkt for potentiel fjederenergi.
Lad den strækning i nu måler være h1,
som er afstanden fra gulvet til der hvor elastikken fæstnes til flasken, når I
har løftet flasken.
Flasken
slippes nu og den højde den når over gulvet h2 måles .
Højden h flasken er faldet beregnes.
Udfyld følgende skema
|
h1/m |
|
|
|
|
|
|
|
|
|
x/m |
|
|
|
|
|
|
|
|
|
h2/m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Lav en powerregression
på ( x, Epot) . Undersøg om regneforskriften er af formen ![]()
Og bestem k ud fra forskriften.
Indtegn grafen for ![]() med det fundne k ,
sammen med grafen for Epot.
med det fundne k ,
sammen med grafen for Epot.
3. forsøg:
Eftervisning af formlen for potentiel fjederenergi.
Omvendt
Bungee Jump. ( udføres efter forsøg 2)
Vi vil her se mere på
energien i en fjeder eller for os energien i en elastik.
Den potentielle fjederenergi der oplagres i
en fjeder er ![]() .
.
Benyt en flaske med vand, lad f.eks. massen af flaske med vand være 200g.
I skal benytte en målestok . Benyt en
elastik på ca. en meter, hæng den højt
op.
Benyt samme elastik som ved forsøg 2.
Start med at lade elastikken hænge frit uden
flaske.

Mål afstanden x0 fra gulvet op til elastikken (absolut
nulpunktet for potentiel fjederenergi).
Sæt dernæst flasken på elastikken, mål
afstanden x1, fra gulvet til hvor flasken hænger i hvile i
ligevægtsstillingen, mål op til der hvor elastikken fæstnes.
Lad x være strækningen elastikken er trukket
ud. Der gælder da ![]() .
.
Dette punkt benyttes faktisk ikke, men det
er rart at vide hvor det er.
I ligevægtsstillingen er ![]() , dvs.
, dvs. ![]() , idet størrelsen af
tyngdekraften er lig størrelsen af fjederkraften.
, idet størrelsen af
tyngdekraften er lig størrelsen af fjederkraften.
Vi vil nu se på bevægelser, hvor flasken
svinger under nulpunktet for potentiel fjederenergi
( altså over det punkt hvor elastikken kan
hænge helt frit uden flaske).
Vi vil udføre et forsøg hvor vi trækker
flasken yderligere ned til højden h1
, slipper flasken og bestemmer højden h som flasken løftes.
Mål højde h1 fra jorden til der
hvor elastikken fæstnes, slip flasken så
den fyrres af opad, mål højden h2 som flasken opnår efter
affyringen.
Lad os betragte situationen inden affyringen
Vi har
![]() , sidste led forsvinder, idet v=0 når flasken
, sidste led forsvinder, idet v=0 når flasken
vender i sin bevægelse, både nede og oppe.
Der gælder da ![]()
x er
her igen strækningen elastikken er trukket ud, målt fra nulpunktet.
Lad os betragte situationen efter affyringen
![]()
Lad nu ![]() være stighøjden for flasken.
være stighøjden for flasken.
Lad x2 være den strækning
elastikken er strukket ud, ved højden h2,
der gælder da
![]()
Hvis vi antager energibevarelse får vi
![]() ó
ó
![]() ó
ó
![]() =>
=>
(3)
![]()
Udfyld følgende skema
|
h1/m |
|
|
|
|
|
|
|
|
|
x/m |
|
|
|
|
|
|
|
|
|
h2/m |
|
|
|
|
|
|
|
|
|
h/m |
|
|
|
|
|
|
|
|
Lav en lineær regression på ( x, h) .
Indtegn
grafen for ![]() i samme koordinatsystem.
i samme koordinatsystem.
Benyt det k som I har bestemt ved forsøg 2.
Sammenlign de to grafer.
Tjek
for fejl ved forsøg 2 og 3
Start med at trække flasken helt ned til
gulvet, slip flasken.
Hvor højt når den op. Kald denne højde hop
Slip nu flasken fra denne højde.
Når den gulvet? Forklar hvorfor, hvis den ikke gør.
I skal nu bestemme hvor højt I skal løfte
flasken, når I slipper flasken må den ikke ramme gulvet, men den skal komme
meget tæt på.
Kald denne højde for hned
Hvad er forskellen på de to højder?
4. forsøg Dæmpet harmonisk bevægelse, find
dæmpningsfaktoren
Teori:
Den mekaniske energi i en fjeder er
(4) ![]() , hvor A er
amplituden.
, hvor A er
amplituden.
Vi vil udlede denne formel:
Der gælder
![]() og
og ![]() .
.
Stedfunktionen og hastighedsfunktionen for
den harmoniske svingning er:
![]() og
og ![]() ,når x(t)=0 hvis t=0
,når x(t)=0 hvis t=0
vi har :
![]() og dermed
og dermed
![]()
Da der gælder : ![]() og
og ![]() har vi
har vi ![]() .
.
Fra matematik ved vi at : ![]() , dette giver :
, dette giver :
![]() qed.
qed.
Vi kan overføre denne formel til en dæmpet
harmonisk svingning.
Bevægelsesligningen for en dæmpet harmonisk
svingning er
![]() , hvor
, hvor ![]() er den dæmpede amplitude.
er den dæmpede amplitude.
Der gælder altså
![]()
og der med
(5) ![]()
på en svingningstid
har vi altså
![]()
Forsøg:

Hæng en flaske med vand i elastikken. Lad
f.eks. massen af flaske med vand være 200g.
Andvend CBL 2 og programmet DATAMATE.
( Eller CBL 1 og programmet Physics, med små
varianter)
Benyt en ultralydssonde.
Forbind ultralydssonden til sonic indgangen på CBL
2’en.
Start DATAMATE programmet.
Vælg 1. setup
Vælg DIG
Vælg MOTION (m)
Under Mode , vælg da 2 Time-graph
Benyt følgende settings: Timeinterval:0,1
Number of samples
100
Vælg 1 ok to gange
Vent til ultralydssonden blinker og klikker
Tast nu 2 start.
Der læses nu følgende ind i listerne:
Tid i L1
Strækning i L6
Hastighed i L7
Acceleration i L8
Læs listerne over i TI-Interactive.
Betragt en graf over (tid, strækning) .
I vil nu kunne se en dæmpet sinusfunktion.
Giv et skøn over perioden på sinusfunktionen.
Benyt dette skøn til at fitte den bedste
sinusfunktion.
Denne har formen:
![]() hvor h vil være
afstanden fra ultralydssonden til bunden af flasken.
hvor h vil være
afstanden fra ultralydssonden til bunden af flasken.
Bemærk at dæmpningen ikke er med, den skal I
selv finde senere.
Benyt den fundne sinusfunktion til at finde
den nøjagtige periode T og fjederkonstanten
k.
Benyt følgende formler :
![]() og
og ![]()
Vi skal nu finde den mekaniske energi i
systemet:
![]()
hvor x er afstanden fra ligevægts stillingen.
Benyt listerne i TI-Interactive
til at finde X som L6-h ,hvor h er afstanden fra ultralydssonden til bunden af
flasken.
Benyt nu listerne i TI-Interactive
til at beregne den mekaniske energi.
Benyt den ovenfor fundne fjederkonstant k.
Tegn nu en graf over ( tid , Emek).
Kommenter grafen.
Lav eksponentiel regression på grafen. Indtegn
den sammen med grafen.
Den eksponentielle regression har formen ![]() omskriv den , så den
har formen
omskriv den , så den
har formen
![]() og find derved
γ.
og find derved
γ.
Find dernæst dæmpningsfaktoren ![]() på stedfunktionen.
på stedfunktionen.
Den endelige stedfunktion har formen
![]() find den og tegn den ind sammen med ( tid, strækning) grafen.
Vurder selv på amplituden.
find den og tegn den ind sammen med ( tid, strækning) grafen.
Vurder selv på amplituden.
5. forsøg : Eftervisning af svingningstidsformlen
, ved anvendelse af accelerometer.
Hæng en plastflaske med vand på elastikken. Noter massen m af flaske med vand
Fyld f.eks. vand i flasken til den samlede
masser er 200g .
Sæt et accelerometer
fast på flasken.
Pilen på acelerometret
skal vende opad.
Benyt en CBL2 og et low-g accelerometer.
Start med at overføre
Datamate Programmet fra CBL2 til TI-83-plus.
Forbind Low-g
accelerometret til CH1 på CBL2’en.
Forbind Lommeregneren med
CBL2’en.
1.
Tænd lommeregneren og start DATAMATE programmet ( det ligger bag APPS-knappen). Tast ![]() for at resette
programmet.
for at resette
programmet.
2. Vælg SETUP fra main screen.
a.
tast ![]() for at vælge .
for at vælge .
b.
Vælg fra listen.
c.
Vælg fra listen.
d.
Vælg for at vende
tilbage til main screen.
3. Accelerometeret
skal nulstilles så det kun viser
flaskens acceleration, det skal vise –
9.8 m/s2 når vi har
et frit fald.
Vælg fra
main screen.
a.
Lad flasken være I hvile med pilen på accelerometret
pegende opad.
b.
Vælg fra .
c.
Vælg fra skærmen.
d.
Når visningen er stabil tastes ![]() .
.
Træk nu flasken 5-10cm ud fra ligevægtsstillingen og slip
flasken så den sættes i svingninger.
4.
Vælg
5. Når dataopsamlingen er afsluttet vil grafen
over accelerationen som funktion af tiden vise sig på lommeregneren.
Grafen vil nu vise en dæmpet harmonisk svingning.
Hvad er svingningstiden ca for bevægelsen?
Der gælder svingningstidsformlen
: ![]() .
.
Stemmer den overens med jeres forsøg?
Husk at få jeres beregninger
lagt ind på dokumentet.
Lav nu en sinusregression på
jeres måletal.
Tegn nu en graf over jeres måletal med regEQ(x) indtegnet
oveni. Passer perioden?
I vil nu kunne se at I
mangler dæmpningen.
Amplituden aftager
eksponentielt. Prøv nu at ændre begyndelsesamplituden til
den begyndelsesamplitude I
kan aflæse på jeres lommeregner.
Gang nu et led ![]() på amplituden ,vælg
μ<1, find det eksponentialled der passer med
jeres graf.
på amplituden ,vælg
μ<1, find det eksponentialled der passer med
jeres graf.
Prøv jer frem eller lav
eksponentiel regression på amplituderne.
Indtegn den graf der passer
bedst i samme grafvindue som jeres måletal.
6.forsøg Bungee Jump med accelerometer
Hæng en plastflaske med vand på elastikken. Noter massen m af flaske med vand
Fyld f.eks. vand i flasken til den samlede
masser er 200g . ( se figur nedenfor)
Sæt et accelerometer
fast på flasken.
Pilen på acelerometret skal vende opad.
Benyt en CBL2 og et low-g accelerometer.
Start med at overføre
Datamate Programmet fra CBL2 til TI-83-plus.
Forbind Low-g
accelerometret til CH1 på CBL2’en.
Forbind Lommeregneren med
CBL2’en.
|
|
2.
Tænd lommeregneren og start DATAMATE programmet ( det ligger bag APPS-knappen). Tast ![]() for at resette
programmet.
for at resette
programmet.
2. Vælg SETUP fra main screen.
e.
tast ![]() for at vælge .
for at vælge .
f.
Vælg fra listen.
g.
Vælg fra listen.
h.
Vælg for at vende
tilbage til main screen.
4. Accelerometeret
skal nulstilles så det kun viser flaskens
acceleration, det skal vise –
9.8 m/s2 når vi har
et frit fald.
Vælg fra
main screen.
e.
Lad flasken være I hvile med pilen på accelerometret
pegende opad.
f.
Vælg fra .
g.
Vælg fra skærmen.
h.
Når visningen er stabil tastes ![]() .
.
4.
Vælg
Løft nu flasken højt op over
ligevægtsstillingen og slip flasken, pas
på at den ikke rammer gulvet.
5.
Når dataopsamlingen er afsluttet vil grafen over
accelerationen som funktion af tiden vise sig på lommeregneren.
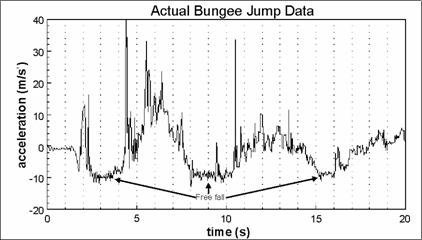
Kommenter grafen.
Teoretiske
overvejelser
Der er anvendt to formler for mekanisk
energi når vi arbejder med fjedre, vi vil vise at de i virkeligheden er ens.
Hvis vi betragter en harmonisk bevægelse
hvor fjederen svinger om sit ligevægtspunk anvender vi formlen for
fjederenergi:
(6) ![]() , hvor x er afstanden til ligevægtspunktet.
, hvor x er afstanden til ligevægtspunktet.
Når fjederenergien regnes fra det absolutte
nulpunkt, så anvender vi følgende mere generelle formel.
(7) ![]()
Vi vil nu vise matematisk, hvorfor vi kan se
bort fra leddet med den potentielle energi i tyngdefeltet, når vi regner
omkring ligevægtspunktet.
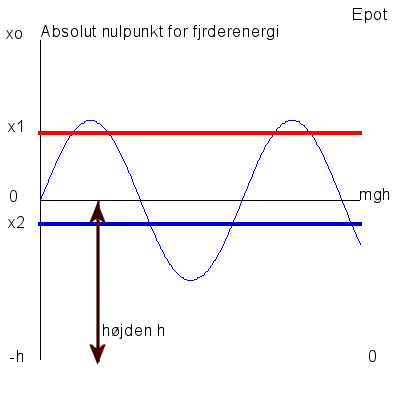
Idet x1 og x2
er tilfældige steder f.eks. hhv. over og
under ligevægtspunktet, målt som afstande til ligevægtspunktet, x2
er altså et negativt tal, hvis punktet ligger under ligevægtspunktet.
Lad x0 være afstanden fra det
absolutte nulpunkt til ligevægtspunktet.
Lad h være afstanden fra nulpunktet for
potentiel energi i tyngdefeltet, op til ligevægtspunktet.
Ser vi på ændringen i mekanisk energi ved
anvendelse af formlen for fjederenergi får vi:
![]()
![]()
![]()
![]()
![]() Vi får derfor vha.
lidt matematik:
Vi får derfor vha.
lidt matematik:
![]()
idet ![]() ifølge Hookes lov fås:
ifølge Hookes lov fås:
![]() og de to beregninger
stemmer altså overens.
og de to beregninger
stemmer altså overens.
EH 13-11-2004