Trafikfysik

 

Frontalt sammenstød

 

Lad os se på hvilke kræfter der virker under et frontalt sammenstød.

 

 

Lad os betragte en bil der kører med farten 90km/t ind i et træ.

 

Lad os antage at accelerationen er konstant under standsningen. Hvis man skal beregne accelerationen benyttes formlen

 

    ,hvor s er den strækning bilen kører efter sammenstødet, altså den længde bilen sammentrykkes.

 

Øvelse 1 : Eftervis at formlen  kan fås vha. ligningerne   og .

 

Ekin  er den kinetiske energi af bilen, hvis bilen kører ind i træet er  F=m*a, hvor m er massen af bilen og a er accelerationen af bilen.

 

Lad os se på hvor meget bilen sammentrykkes, altså lad os finde strækningen s.

 

 

 

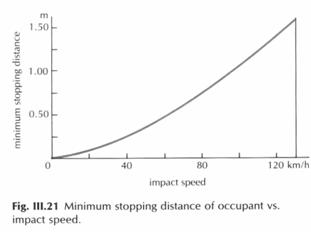På figuren III.21 kan man se at hvis farten er ca. 90km/t, så vil stoppedistancen være ca. 0,75 m.

 

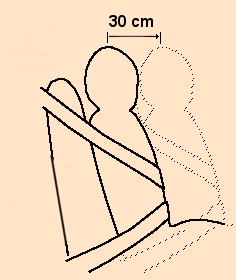Selen strækker sig ca 30 cm , hvilket sammenlagt giver en strækning s= 1,05m

Omregner vi  90km/t til 25m/s, og benyttes formlen  , så fås a= 297m/s2=30g.

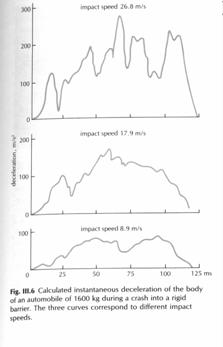Disse tal passer med ovenstående grafer fig III.6

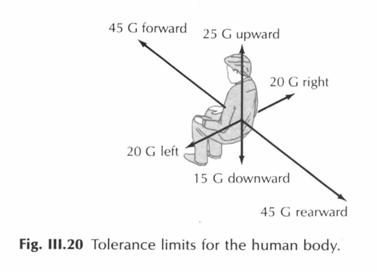
På figur III.20  kan man se hvad en person kan tåle:

 

Så man kan konkludere at det er på grænsen.

Person mærker kraften F=m*a, hvor m er massen af personen, hvis personen vejer 70 kg

bliver det altså  F=20790N fordelt over selerne, hvis man har sele på, og fordelt over airbagen som alle nye biler har.

 

Øvelse 2. Find accelerationen udtrykt i antal g, for en bil der kører med farten 60km/t ind i et træ.

 

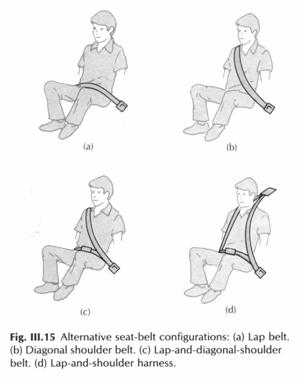
Øvelse 3. Se på  figurerne  III.11, III.5 , III.16 og figur 9. Forklar hvad du ser, hvilke seletyper er de bedste?

 

Der gælder ,  løses   fås at sammenstødet varer 80ms.

Øvelse 4. Hvor længe varer sammenstødet , for en bilen der kører med farten 60km/t ind i et træ.

 

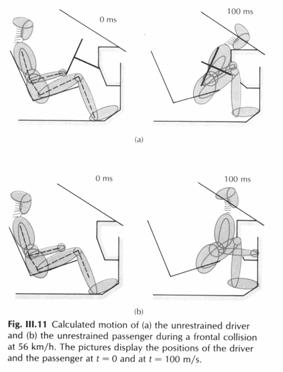
Personen mærker altså accelerationen på 30 G i 84ms. Sammenlign med grafen over selerne.

 

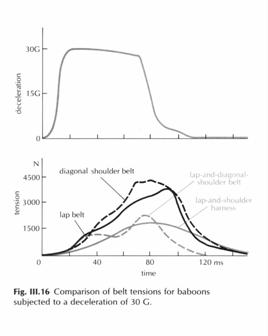
Figur 9

    

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Øvelse 5 : Eftervis at formlen , kan fås ud fra bevægelsesligningerne for frit fald:  og . ( samme formel anden gang).

 

Øvelse 6 :Eftervis at det passer at hvis man kører med 90km/t ind i et træ så svarer det til et frit fald fra 11 sal.

 

Impuls

 

 

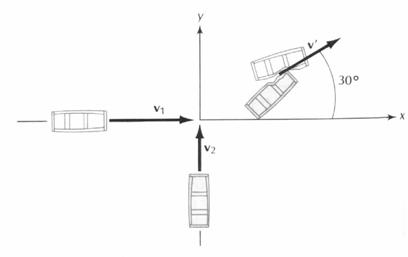
Figur 11

 

To biler støder sammen, før sammenstødet har bilerne hastighederne

v1  ( kaldet hvid bil ) og v2 kaldet ( sort bil), umiddelbart efter sammenstødet har begge biler hastigheden vefter.

 

 

 

 

 

Løsning: Den hvide bil har hastigheden v1, som er rettet i x-retningen, den sorte bil har hastigheden v2, som er rettet i y-retningen.

Impulsen før er 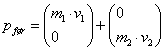 , impulsen efter er lig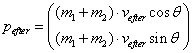

Impulsbevarelse giver således ligningerne:

(1)    og (2) 

 

 

 

Eksempel:

 

En hvid bil har massen 1100kg, og en sort bil har massen 1300kg, de støder sammen i et kryds som på figur 11, den sorte bil kører mod Nord. Efter kollisionen er deres bremsespor 18.7 meter langt, i en retning 30 ° Nord. Har nogle af bilerne overskredet hastighedsgrænsen på 25m/s ( 90km/t)? Antag at begge bilerne blokerer på bremserne, og at gnidningskoefficienten på underlaget er μ=0,8.

 

Før vi kan finde hastighederne v1  og v2, så skal vi kende vefter, den finder vi ud fra bremselængden .

Accelerationen af de sammenkørende biler er:

 

.

 

Eksempel

For retlinet bevægelse med konstant acceleration gælder der

, vis at det med begyndelses værdierne v0=vefter, v=0, s0=0, s=l giver   ( samme formel tredje gang)

 

Vi har derfor  

Ligning 1) og 2) giver således

 

 

 

 

Den hvide bil havde  altså for meget fart på.

 

Øvelse 7.

Hvilke hastigheder ville bilerne have haft hvis bremsesporet havde været 25m med en vinkel på 50° Nord?

 

Overhaling.

 

Lad os betragte en Rød Megane Renaut Sport der er ude at køre tur på en landevej

med fartbegrænsningen 80km/t. I dens vejbane ligger en grøn bil 15 m foran, den kører 70km/t, den røde bil tvinges ned til 70km/t og vil nu overhale, i modkørende vejbane kommer en modkørende bil 300m væk, den kører med 80km/t. Kan føreren af den røde bil overhale uden at køre ind i den modkørende bil?

Der er i det følgende regnet fra midten af bilerne så vi slipper for at medregne billængderne.

 

Tiden  fra t=0sek  til t= 1,3sek.

Den røde bil har accelerationen 0-100km/t på 6,5 sek., altså a=4,27m/s2.

Den skal først accelerere fra 70km/t op til 90km/t, altså fra 19,44m/s til 25m/s.

Ligningen    giver her .

Ligningen  giver at den røde bil under accelerationen har kørt 3,6m+25,27m= 28,9m.

Den grønne  bil er i mellemtiden nået strækningen .

Den grønne bil er altså efter 1,3 sek.   11,4m foran den røde bil.

 

Tiden fra 1,3 sek. til 8,7sek.

Den røde bil skal være 30 meter foran den grønne bil, for at kunne komme ind uden at genere.

Hvis vi nulstiller tiden og strækningen har vi altså nu ligningen

  hvilket med vrød=25m/s og vgrøn=19,44m/s  giver t=7,44sek.

Den røde bil har altså yderligere kørt 186m.

Den samlede strækning den røde bil har kørt under overhalingen er altså 28,9m+186m=215m

Overhalingen tage samlet 1,3sek+7,44sek=8,7sek.

 

Den modkørende bil har på denne tid kørt med hastigheden 22,22m/s, altså 193m.

300m-193m= 107m, hvilket vil sige at den røde bil ( eller den modkørende bil) skal ind i rabatten for at undgå et sammenstød.

 

Øvelse 8.

Lad os betragte en Rød bil med accelerationen a=2,3m/s2.

Den er ude at køre tur på en landevej med fartbegrænsningen 80km/t. I dens vejbane ligger en grøn bil 15 m foran, den kører 80km/t, den røde bil kører også 80km/t men vil nu overhale,  i modkørende vejbane kommer en modkørende bil 400m væk, den kører med farten 90km/t. Kan føreren af den røde bil overhale uden at køre ind i den modkørende bil?

 

Kilde : Ohanian Physics Second Edition expanded1989

 

EH  16 Nov. 04